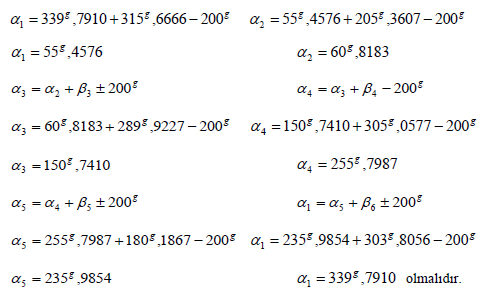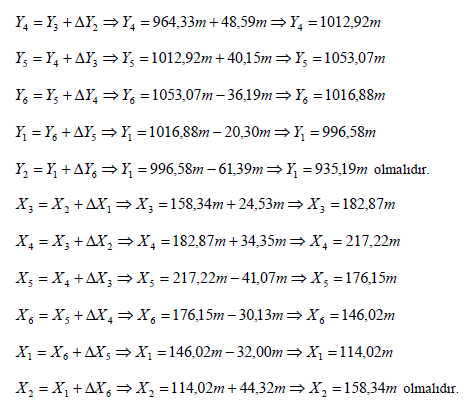Açık, kapalı ve dayalı (bağlı) poligon hesapları nasıl yapılır ve kaba kenar hatalarının giderilmesini gibi temel bilgileri ele alacağız.

A. AÇIK POLİGON HESABI

Açık poligon geçkisi (güzergâhı), bir nirengi veya poligon noktasından başlayarak koordinatları belli olmayan başka bir noktada sona erer. Bu poligonların hesabını kontrollü yapmak mümkün değildir. Onun için bir zorunluluk olmadıkça kullanılmazlar. Eğer kullanılacaksa açı ve kenarlar kontrollü olarak ölçülmelidir.
Açık poligon hesabı için birinci temel ödevin her poligon noktasında bir defa tekrar edilmesidir diyebiliriz.

Geçki örneği,

A.1. Ölçülen Değerlerin Tabloya Yazılması
Koordinatları bilinen bir B noktasından itibaren üç noktalı bir açık poligon geçkisi (güzergâhı) düşünelim (Şekil 1). 1,2 ve 3 nu.lı poligon noktalarının koordinatlarının hesaplanabilmesi için a1 semt açısı ile S1 kenarının uzunluğunun bilinmesi gerekir.
Arazide poligonun β0 , β1, β2 kırılma açıları ile S1 , S2 , S3 uzunlukları ölçülür. Ölçülen bu değerler Tablo 1‟de görüldüğü gibi yazılır.
Örnek 1: Şekil 1‟e göre gerekli ölçüleri verilen açık poligon hesabının verilerinin
tabloya nasıl yerleştirildiğini görelim.

Verilenler:

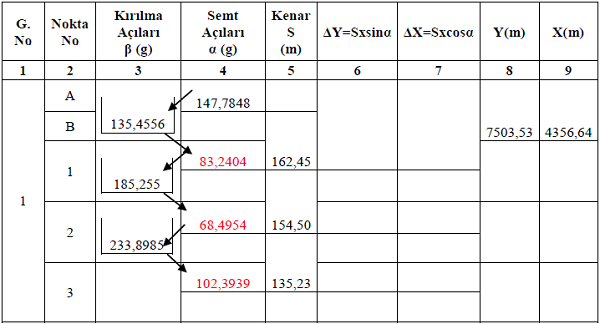
(AB)= a0 =147g,7848 1    S = 162,45 m         Xb= 4356,64 m
β0= 135g,4556                  S2 = 154,50 m        Yb= 7503,53 m
β1= 185g,2550                   S3 = 135,23 m
β2= 233g,8985

A.2. Semt Açılarının Hesabı
Poligon semt açısının hesabı için bir evvelki semt açısı ile poligon açısı toplanır. Elde edilen açı 200 graddan küçük ise buna 200 grad eklenir. 200 graddan büyük ise 200 grad çıkarılır. Bu işlemden sonra geri kalan açı 400 graddan büyük ise bundan tekrar 400 grad çıkarılır. Bu kurala göre semt açısı elde edilir. Verilenler ilgili yerlerine yerleştirilerek 4. sütundaki semt açıları üçüncü temel ödeve
göre bulunur.
135g,4556 + 147g,7848 = 283g,2404

200 graddan büyük olduğu için 200 grad çıkarılır ve 83g,2404 olarak bulunur. Diğer
semt açıları da tabloda olduğu gibi hesaplanır.

A.3. Koordinat Farklarının Hesabı
6‟ncı sütuna 4‟üncü sütundaki semt açılarının sinüs değerleri yazılır ve 5‟inci
sütundaki kenarlar ile çarpılarak ΔY değeri bulunur. 7‟nci sütuna ise 4‟üncü sütundaki semt
açılarının kosinüs değerleri yazılır ve 5‟inci sütundaki kenarlar ile çarpılarak ΔX değeri
bulunur. ΔX ve ΔY değerlerinin işaretleri semtlerin bulundukları trigonometrik daire
bölgelerine göre tayin edilir (Tablo 3).

ΔX=162,45*cos83,2404    ΔY=162,45*sin83,2404
ΔX=+42,27 m                      ΔY=+156,85 m

Diğer ΔX ve ΔY değerleri de yukarıda anlatıldığı gibi hesaplanır.

A.4. Koordinatların Hesabı
Bulunan ΔX ve ΔY değerleri 8 ve 9‟uncu sütunlardaki Y ve X değerlerine,
işaretlerine göre eklenip veya çıkarılarak yeni noktaların koordinatları bulunur.

B. DAYALI (BAĞLI) POLİGON HESABI

Dayalı (bağlı) poligon geçkisi, koordinatları bilinen bir nirengi veya poligon noktasından başlayıp yine koordinatları bilinen bir nirengi veya poligon noktasında sona erer. Bağlı poligon hesabında hesabın kontrolü yapılabilir. Bu şekildeki geçkide açı ve kenar ölçümündeki kaba hatalar ortaya çıkacağından hata sınırı içinde kalan hataların ölçülere dağıtılmaları mümkündür.
Bağlı poligon hesabı aynen yukarıda gördüğümüz açık poligon hesabında olduğu gibi yapılır. Ancak hesaplanan son noktanın başka noktaya olan semti ile koordinatları belli olduğundan hesapların kontrolü yapılabilir.

Geçki örneği,

B.1. Ölçülen Değerlerin Tabloya Yazılması
Koordinatları bilinen A, B, C ve D noktaları, a0 =(AB) baştaki semt açısı ile an semt açıları verilen iki noktalı bir bağlı (dayalı) poligon güzergâhı düĢünelim (Şekil A). 1 ve 2 numaralı poligon noktalarının koordinatlarının hesaplanabilmesi için (AB)= a0 semt açısı, an semt açıları ile S1 , S2 , S3 ve poligon kırılma açılarının bilinmesi gerekir. Arazide poligonun β0, β1, β2 kırılma açıları ile S1 , S2 , S3 uzunlukları ölçülür. Verilen ve ölçülen bu değerler Tablo A“da olduğu gibi yazılır.
Örnek A: Şekil A‟daki dayalı (bağlı) poligon geçkisine göre verilen ölçülerin hesap tablosuna yazılışını gösteriniz.

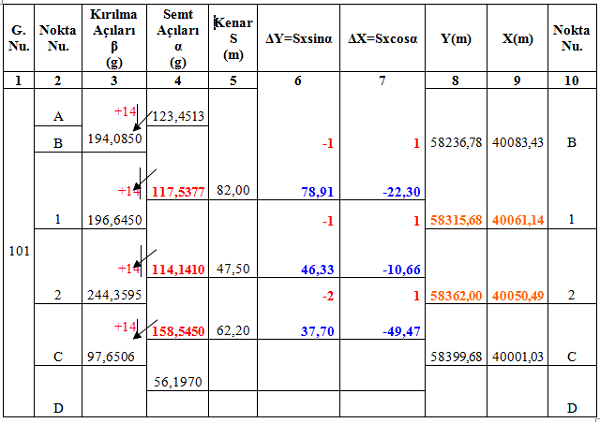
(AB)= a0 =123g,4513              (CD)= an =56g,1970         S1 = 82,00m          b Y 58236,78m
β0= 194g,0850                                                                         S2 = 47,50m         b X 40083,43m
β1 = 196g,6450                                                                         S3= 62,20m          c Y 58399,68m
β2= 244g,3595                                                                                                          c X 40001,03m
β3= 97g,6506

B.2. Semt Açılarının Hesabı
Şekil A‘da (an) , poligonun bağlandığı C noktasından D noktasına olan (CD) semti olup bu değer ya verilmiştir veya C ve D noktalarının koordinatları yardımıyla ikinci temel ödeve göre hesaplanır. Bağlı poligon hesabındaki semtler;

a1= a0+β0±200g , a2= a1+β1±200g , a3= a2+β2±200g , a4= a3+β3±200g … şeklinde hesaplanır.

Yukarıdaki eşitlikleri taraf tarafa toplarsak eşitliğin her iki tarafında bulunan a1 ,a2 , a3 ve a4 semt açıları birbirlerini götürür. ‘β’ kırılma açılarının toplamını da [β] şeklinde gösterecek olursak;

fβ=a0+[β]±n*200g bu formülde a0 semt açısını eşitliğin sol tarafına alarak, fβ-a0=[β]±n*200g formülünü bulmuş oluruz.

n= kırılma açılarının sayısı f= kırılma açılarında yapılan hata miktarı  a0= baştaki semt açısı an= sondaki semt açısı

Kural
Bağlı poligon hesabında başlangıç semti ile bütün poligon açıları toplanır ve bulunan toplamdan gereği kadar 200 grad çıkarılırsa son semt açısı bulunur veya son semt açısı ile başlangıç semt açısının farkı, bütün poligon açılarının toplamından gereği kadar 200 grad ve katları çıkarıldıktan sonra kalan miktara eşit olur.

Aşağıda verilen Tablo B’de, Örnek A‘da verilenlere göre semt açılarının bulunuşu yapılmıştır.

İlk önce [β] bulunur. [β] =856g,1914 olur.

fβ=a0+[β]±n*200g => fβ=123 ,4513g + 732 ,7401g 4*200g => an-a0=56 ,1914g olur.

Açı ölçümünde hata miktarı fβ= 56 ,1970g – 56 ,1914g = 0 ,0056g yani 56 saniyedir. 56/4 = +14 saniye olarak her bir kırılma açısına hata dağıtılır. Dağıtıldıktan sonra düzeltilmiş poligon kırılma açıları ile ilk semt açısı toplanır ve gerekli çıkartma yapılarak gereken semt açısı bulunur. Bu işlem sonuna kadar tekrarlanır. Elde edilen son semt değeri, an semti ile aynı değerde olmalıdır.

Poligon Kırılma Açıları                              Düzeltilmiş Poligon Kırılma Açıları
β0= 194g,0850                                                    β0= 194g,0864
β1= 196g,6450                                                     β1= 196g,6464
β2= 244g,3595                                                    β2= 244g,3609
β3= 97g,6506                                                      β3= 97g,6520

Ölçümlerde yapılan hata miktarı yönetmeliğin verdiği hata miktarından küçük olmadır. Yani fβ < Fβ olmalıdır.

Fβ=1c+(150/[β])*(n-1)*√n  -> c: Grad dakikası

[S]= Kenarların toplamı    [S]= 191,70 m

Fβ=1c+(150/[191,70 m])*(4-1)*√4   ->  Fβ= 1c+4 c,69  ->  Fβ= 5 69c= 569cc -> cc: Grad saniyesi

fβ < Fβ olur. O zaman ölçülen değerler hata sınırı içindedir. Kabul edilebilir.

B.3. Semt Açılarının Hesap Kontrolü
Hatalar dağıtıldıktan sonra ilk semt açısı ile (123g,4513) ilk düzeltilmiş poligon kırılma açısı (194g,0864) toplanarak 3. temel ödeve göre ikinci semt açısı (a1) hesaplanır. Diğer semt açıları da aynı yöntemle hesaplanır. Hesaplanan semt açıları son semt açısına eşit olmalıdır.

a1= a0+β0±200g -> a1= 123g 4513+194g,0864-200g -> a1= 117g,5377

a2= a1+β1±200g-> a2= 117g,5377+196g,6464-200g -> a2= 114g,1410

a3= a2+β2±200g-> a3= 114g,1410+244g,3609-200g -> a3= 158g,5450

an= a3+β3±200g-> an= 158g,5450+97g,6520-200g -> an= 56g,1970 olur.

B.4. Koordinat Farklarının Hesabı
6 numaralı sütuna 4 numaralı sütundaki semt açılarının sinüs değerleri yazılır ve 5 numaralı sütundaki kenar değerleri ile çarpılarak ΔY değeri bulunur. 7 numaralı sütuna ise 4 numaralı sütundaki semt açılarının kosinüs değerleri yazılır ve 5 numaralı sütundaki kenarlar ile çarpılarak ΔX değeri bulunur. ΔX ve ΔY değerlerinin işaretleri semt açılarının bulundukları trigonometrik daire bölgelerine göre tayin edilir (Tablo C).

ΔX1=82,00m*cos117g,5377    ΔY1=82,00m*sin117g,5377
ΔX1=-22,30 m                           ΔY1=+78,91 m

Diğer ΔX ve ΔY değerleri de yukarıdaki gibi hesaplanır ve tabloda yerlerine yazılır.

Kural
Bağlı poligon hesabında hesap edilen koordinat farklarının toplamı son noktanın koordinatlarından ilk noktanın koordinatlarının çıkarılması ile elde edilen farka eşittir. ΔX ve ΔY değerleri alt alta, ayrı ayrı toplanır.

[ΔY] =+162.94m  [ΔX]= -82,43m Sonra koordinatları bilinen X ve Y değerlerinin farkları alınır.

FY=Yc-Yb= 58399,68m-58236,78m -> FY=+162,90m

FX=Xc-Xb= 40001,03m-40083,43m -> FX=-82,40m

B.5. Hata Hesabı ve Dağıtımı
Gerek açı ölçülerinde gerekse kenar ölçülerindeki düzensiz hatalar nedeniyle uygulamada bu teorik durum gerçekleşmez. Bunun sonunda;

B.6. Koordinatlarının Hesabı
Kenarlara hatalar dağıtıldıktan sonra sıra kesin koordinatları hesaplamaya gelmiştir.

Y1= YB+ ΔY1 -> Y1=58236,78m+78,90m -> Y1=58315,68m

Y2= Y1+ ΔY2 -> Y2=58315,68m+46,32m -> Y2=58362,00m

Yc= Y2+ ΔY -> Yc=58362,00m+37,68m -> Yc=58399,68m

X1= XB+ ΔX1 -> X1=40083,43m-22,29m -> X1=40061,14m

X2= X1+ ΔX2 -> X2=40061,14m-10,65m -> X2=40050,49m

Xc= X2+ ΔX -> Xc=40050,49m-49,46m -> Xc=40001,03m

C.KAPALI POLİGON HESABI
Kapalı poligon geçkilerindeki poligon hesabı, bağlı poligon geçkilerinde yapılan poligon hesapları gibi yapılır. Ancak kapalı poligon geçkisi başladığı noktada son bulduğu için kontrol formülleri küçük bir değişiklik gösterir.

a1-a0= [β0]±n*200g semt kontrol formüllerinde kapalı poligonun başlangıç ve son semti aynı olacağından an-a0’dır.
Buna göre; 0= [β0]±n*200g olur.

C.1. Ölçülen Değerlerin Tabloya Yazılması
Koordinatları bilinen A veya 1, a0 baştaki semt veya a1 semtleri verilen bir kapalı poligon geçkisi düşünelim (Şekil 1) 2, 3, 4, 5 ve 6 nu.lı poligon noktalarının koordinatlarının hesaplanabilmesi için(1–2)=a1 semt açısı ile S1,S2,S3,S4,S5,S6 ve poligon kırılma açılarının bilinmesi gerekir. Arazide poligonun β1,β2,β3,β4,β5,β6 kırılma açıları ile S1,S2,S3,S4,S5,S6 uzunlukları ölçülür. Verilen ve ölçülen bu değerler Tablo 1’de olduğu gibi yazılır.

Örnek 1: Şekil 1‟deki kapalı poligon geçkisine göre verilen gerekli ölçülerin tabloda yazılışını görelim.

Verilenler: (1–2)=a1=339g,7910

β1= 315g,6550                                                    S1= 38,08 m                      Y1= 935,19 m
β2= 205g,3590                                                  S2= 59,49 m                      X1= 158,34 m
β3= 289g,9210                                                   S3= 57,43 m
β4= 305g,0560                                                  S4= 47,10 m
β5= 180g,1850                                                   S5= 37,91 m
β6= 303g,8040                                                  S6= 75,73 m

İstenenler: 3, 4, 5, 6 ve 1 numaralı noktaların koordinatlarını (Y ve X değerlerini)
hesaplayalım. İlk önce verilenler dikkatli olarak hesap tablosuna yerleştirilir. Daha sonra açı kontrolü yapılır. Açı kontrolü poligon açıları toplanarak yapılır.

Bu toplamın iç açılar toplanıyor ise [βiç]=(n-2)*200g , dış açılar toplanıyor ise [βdış]=(n+2)*200g formüllerin verdiği miktarda olması gerekir.

C.2. Semt Açılarının Hesabı
Kapalı poligon bir çokgen olduğu için açı kontrolü, iç veya dış açıların toplamı şeklinde de yapılabilir. Bir kapalı poligon, o poligonu teşkil eden noktaların iki eksiği kadar üçgene ayrılacağı için iç açıların toplamı poligonu teşkil eden nokta adedinin iki eksiğinin 200g ile çarpımına eşittir.

[βiç]=(n-2)*200g dış açılar toplanıyor ise [βdış]=(n+2)*200g formüller ile bulunur. Bu formüllerde “n” poligon geçkisini teşkil eden nokta sayısıdır. Poligon kırılma açılarında yapılan düzensiz hatalar yönetmeliğin verdiği izin kadar olmalıdır. Buna göre yönetmelikte yapabileceğimiz maksimum hata miktarı aşağıda verilen
formülle hesaplanır. Fβ=1c+(150/[β])*(n-1)*√n 

Yapılan hata, bu formülde bulunan değerden küçük olmalıdır. Yani FB<FBmax olmalıdır.

C.3. Semt Açılarının Hesap Kontrolü
Hatalar dağıtıldıktan sonra ilk semt açısı ile (339g,7910) ilk düzeltilmiş poligon kırılma açısı (315g,6666) toplanarak 3. temel ödeve göre ikinci semt açısı ( a1 ) hesaplanır. Diğer semt açıları da aynı yöntemle hesaplanır. Kapalı poligon hesabında hesaplanan semt açıları ilk semte eşit olmalıdır.

C.4. Koordinat Farklarının Hesabı
6 numaralı sütuna 4 numaralı sütundaki semt açılarının sinüs değerleri yazılır ve 5 numaralı sütundaki kenarlar ile çarpılarak ΔY değeri bulunur. 7 numaralı sütuna ise 4 numaralı sütundaki semt açılarının kosinüs değerleri yazılır ve 5 numaralı sütundaki kenarlar ile çarpılarak ΔX değeri bulunur. ΔX ve ΔY değerlerinin işaretleri semtlerin bulundukları trigonometrik daire bölgelerine göre tayin edilir (Tablo 3).

ΔX1=38,08m*cos55g,4576    ΔY1=38,08m*sin55g,4576
ΔX1=+24,52 m                          ΔY1=+29,13 m

Diğer ΔX ve ΔY değerleri de yukarıdaki gibi hesaplanır ve tabloda yerlerine yazılır.

C.5. Hesap Kontrolü
Poligon geçkisinin başlangıç ve bitim noktalarının koordinatları aynı olduğu için ΔY ve ΔX’lerin toplamlarının sıfıra eşit olması gerekir. [ΔY]=0 , [ΔX]=0

D. KABA AÇI HATASI
Bir poligon geçkisinde kaba açı hatasının olup olmadığı açıklık açısı (semt açısı) kontrolü ile anlaşılır. Başlangıç açıklık açısına kırılma açıları eklenir ve ( n*200g ) çıkarıldığında son açıklık açısı bulunmazsa yani büyük bir fark varsa kaba açı hatası var demektir.

4.1. Başlangıçtan Bitiş Yönüne Doğru Poligon Hesabı

Şekil 1‘de görüldüğü gibi 3 numaralı poligon noktasında β3 açısının ölçümünde Δβ kadar kaba hata yapılmış ise ve hesaba B poligon noktasından başlanırsa βb, β1, β2 açıları ile S1,S2,S3 kenarları hatasız olacağından 1, 2, 3 poligon noktalarının koordinatları hatasız elde edilecektir. Diğer taraftan β3 hatalı olduğundan (34), (45) ve (5C) açıklık
açıları hatalı olacak, dolayısıyla 4 numaralı poligon noktası 4′ , 5 numaralı poligon noktası 5′ , ve C nirengi noktası da C’ olarak kayacaktır. Hatalı açının bulunduğu noktayı hesap yoluyla bulmak için hatalı değerlerle açı hata dağıtımı yapmadan poligon geçkisi bir kere B poligon noktasından başlayarak çözülür.
Aşağıdaki çözüm ise sadece tablo üzerinde yapılmıştır (Tablo 1).

D.2. Bitişten Başlangıç Yönüne Doğru Poligon Hesabı
Hesaba C poligon noktasından başlanırsa βc, β5, β4 açıları ile S6,S5,S4 kenarları hatasız olduklarından 5, 4 ve 3 poligon noktalarının koordinatları hatasız elde edilecektir. Diğer taraftan β3 kırılma açısı hatalı olduğundan 2 numaralı poligon noktası 2′ 1 numaralı poligon noktası 1′ ve B nirengi noktası da B’ olarak kayacaktır.
Hatalı açının bulunduğu noktayı hesap yoluyla bulmak için hatalı değerlerle açı hata dağıtımı yapmadan poligon geçkisi bir kere C poligon noktasından başlayarak çözülür.
Aşağıdaki çözüm ise sadece tablo üzerinde yapılmıştır (Tablo 2).

D.3. Açı Ölçüm Hatası Olan Noktanın Bulunması
Hem B poligon noktasından başlanarak hem de C poligon noktasından başlanarak
yapılan hesap sonucu koordinatların her ikisinde de yaklaşık olarak eşit olan noktadaki açıda
kaba açı hatası var diyoruz. Bu nedenle Tablo 1′de ve Tablo 2′de yapılan hesap sonucu 2. poligon noktasının
koordinatları yaklaşık olarak aynı çıktığına göre β2 açısı yanlış ölçülmüştür. Yani;

Hata: 394g,4620-294g,4220=100g,0400’dır.